情報処理の基礎をおさらいする vol.1
新年度がスタートしました。
企業さんには新人が配属され、昨日とは違う何かが職場にあふれているのではないでしょうか。
E.P.ラボでは自分の振り返りを兼ねて、基礎から情報処理~プログラミングについておさらいしたいと思います。何かのお役に立てれば幸いです。
では早速の初回ですが、ビットと2進数についてです。
ビット
コンピュータ(情報処理)の世界ではデータを電荷の状態(キャパシタに電荷がたまっている状態を1、電荷が無い状態を0)で表現します。
![]() ビット0の状態と
ビット0の状態と![]() ビット1の状態
ビット1の状態
これを情報に置き換えたものが最少単位:ビットです。1ビットは’0’もしくは’1’の状態(2種類)を持てます。情報量が2ビットであれば{00,01,10,11}の4種類を表現できます。数値に置き換えると0~3に相当しますね。
2進数
「N進数」ではN種類の記号を用いて数値を表現します。2進数であれば、’0’と’1’の2種類で表現します(‘0’と’1’の状態を持つビットととの繋がりが見えてきましたね)。試しに3という10進数を2進数で表現してみると…
$latex 3_{(10)}=2+1=1*2^1+1*2^0=11\ _{(2)} &s=-1$
となります。(下付のカッコ内は何進数かを意味しています)
この場合11(2)のように2桁の2進数で表現されていることから「10進数の3を2進数で表現するには2ビット必要である」と表現できます。ある数値を2進数N桁で表現できるとき、その情報量はNビットであると言い換えることもできます。
試しに10進数の100を2進数で表現するとどうなるでしょうか?
$latex 100_{(10)}=64+32+4=1*2^6+1*2^5+0*2^4+0*2^3+1*2^2+0*2^1+0*2^0=1100100\ _{(2)}&s=-1$
上記より、10進数の100を2進数で表現すると1100100(2)、情報量は7ビットであることが分かります。
それでは10進数について振り返ってみましょう。10進数は’0’~’9’の10種類の記号を用いて10のn乗で表現します。例えば127(10)を展開すると…
$latex 127_{(10)} = 100+20+7=1*10^2+2*10^1+7*10^0&s=-1$
となります。更に2進数へ展開すると…
$latex 64+32+16+8+4+2+1=1*2^6+1*2^5+1*2^4+1*2^3+1*2^2+1*2^1+1*2^0\\=1111111_{(2)}&s=-1$
となり、10進数も2進数も表現方法は違えど、考え方は同じであることが分かります。
余談ですが127(10)は1111111(2)であることから情報量7ビットであるのと同時に、7ビットで表現できる最大の数となります。7ビットで取り扱える数は0~127(10)の128種類ということですね。
ビットとバイト
コンピューターはビット単位から始まり、4ビット単位、8ビット単位と徐々に取り扱える情報量が増えてきました。4ビットを情報単位とするときはニブル(nibble)、8ビットを情報単位とするときはバイト(Byte)と呼びます。
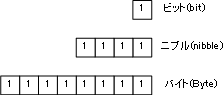
とはいえ、4bitマイコンは最早手に入らないでしょうからニブルを扱うことはまずないでしょう。
皆さんの身の回りで考えると、数年前からWidowsでも64bit版が普及しています。これは一回の命令で取り扱える情報量が64bit(8Byte)であることを意味しています。従来は32bit(4Byte)だったので、情報量だけ見ると64bit OSでは32bit OSの1/2の命令数で済むことになります(実際はそんな簡単ではありませんが…)。
情報量の単位
情報量の単位について考えます。
一般的(10進数)には103をキロ、106をメガ、109をギガと呼びますが、情報の世界(2進数)では210をキロ、220をメガ、230をギガとして取扱います。
256kB(B:バイト、1バイトは8*1ビット)のROMと言われたら、256×210なので262144バイトになります。256×103の256000バイトではありません。
210は1024、220は1048576、230は1073741824となりますから、10進数のキロ、メガ、ギガとは大きく異なります。
Windowsのファイルをエクスプローラと詳細(プロパティ)で比較したとき、サイズが異なることに気が付いた方がいらっしゃると思います。エクスプローラでは72KBと書かれているのに、詳細(プロパティ)を見ると73728バイトとなっています。73728バイトなら73KBじゃないか!と思いますが、情報量のキロは210(1024)なので、73728を1024で割ると72(KB)になるのです。


